Εφαρμογές του Κύκλου των 5ων

[STEFANOS604]

‘’Γραμμικός‘’ Κύκλος των 5ων 
Οι αρχάριοι φτιάξτε τον ‘’κανόνα’’ που δείχνω στο Video εκτυπώνοντας τη φωτογραφία απ' την ''περιγραφή'' στο youtube...

! No longer available

Πώς θα βρω τι ακόρντα απαιτεί ένα φωνητικό, οργανικό ή σύνθετο μουσικό κομμάτι που ακούω από CD…ή πώς θα εναρμονίσω μια μελωδία (πάνω στις νότες που εγώ παίζω με τις χορδές Εκαντίνι και Σί της κιθάρας ή ακούγοντας μόνο μελωδία παιγμένη από άλλα όργανα σε CD…)  ώστε να προκύπτουν συγχορδίες που να είναι ακουστικά (τουλάχιστον στην αρχή της εκμάθησης) υποφερτές ; Ακούμε τη μελωδία και προσπαθούμε να βρούμε την τονική (να βρούμε τον τόνο). Το σπουδαιότερο κριτήριο είναι το "καλό αυτί". Πάντως η γνώση αυτή αποκτάται με μελέτη και την εμπειρία σας στο όργανο. Στην αρχή θα κάνετε λάθη (λογικό) απλά να μην υπάρχει εκνευρισμός. Ανάλογα με το "αυτί" μπορεί να σας πάρει από λίγες βδομάδες μέχρι και μήνες.
Δεν γίνεται χωρίς "καλό αυτί" να τα μάθετε από τη μια μέρα στην άλλη. Επιμονή, υπομονή και σύντομα θα βρίσκετε όχι μόνο την τονική αλλά και όλες τις συγχορδίες.
Πολλές φορές ένα τραγούδι μπορεί να ξεκινάει με την τονική συγχορδία, αλλά αυτό δεν συμβαίνει πάντα. Συνήθως όμως το τέλειωμα του είναι η τονική.
Κύκλος των 5ων στο κλειδί του F (bass)



Κύκλος των 5ων και Tονικότητα Κλιμάκων : ΕΔΩ :
Ποιά είναι η τονικότητα της παρακάτω κλίμακας? Εξήγηση για τον οπλισμό




Η κλίμακα αυτή έχει οπλισμό Bb και Eb αλλά και F# μέσα στο μουσικό κομμάτι. Για επεξήγηση δείτε τη φωτογραφία:





Από τη φωτογραφία  φαίνεται:
Οι 2 υφέσεις είναι στο μεσαίο κύκλο στο G (που είναι το Gm φυσικό) και στον εξωτερικό κύκλο φαίνεται ότι έχει τον οπλισμό της ματζόρε κλίμακας Bb , στον δε εσωτερικό κύκλο (που πρόσθεσα εγώ) έχει F# που είναι ο προσαγωγέας .
Άρα η κλίμακα της φωτογραφίας είναι η Gm ΑΡΜΟΝΙΚΟ. (έχει : Bb , Eb , F#). Δηλαδή:
G A Bb C D Eb F# G η ανιούσα Gm Αρμονικό και
G F# Eb D C Bb A G η κατιούσα Gm Αρμονικό.
Κύκλος των 5ων και Σχετικές κλίμακεςΗ κλίμακα της οποίας η 3η και η 6η βαθμίδα σχηματίζει με την τονική μεγάλα διαστήματα (Μεγάλη 3η και Μεγάλη 6η) λέγεται Ματζόρε (μείζων) κλίμακα.
Η κλίμακα της οποίας η 3η και η 6η  βαθμίδα σχηματίζει με την τονική μικρά διαστήματα (Μικρή 3η και Μικρή 6η ) λέγεται Μινόρε (ελάσσων) κλίμακα.







Κύκλος των 5ων και Νότες Συγχορδιών


Διαφορά της Ματζόρε κλίμακας από τη ΣΧΕΤΙΚΗ Μινόρε
Η κλίμακα της οποίας η 3η και η 6η βαθμίδα σχηματίζει με την τονική μεγάλα διαστήματα (Μεγάλη 3η και Μεγάλη 6η) λέγεται Ματζόρε (μείζων) κλίμακα.
Η κλίμακα της οποίας η 3η και η 6η  βαθμίδα σχηματίζει με την τονική μικρά διαστήματα (Μικρή 3η και Μικρή 6η ) λέγεται Μινόρε (ελάσσων) κλίμακα.



Στα ρυθμικά σχήματα με κιθάρα , κυρίως στα ρεμπέτικα 2/4 (χασάπικα , χασαποσέρβικα , μπάλο , τσιφτετέλι, μπαγιό, σούστα..) και στα 9/8 – ζεϊμπέκικα όλων των μορφών (κλασσικά , μοντέρνα , καμηλιέρικα , απτάλικα ) η κιθάρα παίζεταισαν ρεμπετοκιθάρα – Δείτε το  εδώ:

! No longer available

Τότε οι κιθαρίστες κάνουν εναλλαγή των μπάσων χορδών ώστε να μην χτυπιέται μόνο η θεμέλιος αλλά εναλλακτικά να χτυπιέται και η 5η και έτσι να αποφεύγεται η μονοτονία.
Όλα αυτά επιτυγχάνονται εύκολα στην κιθάρα παίζοντας το ακόρντο της τονικής και συνοδεύοντας και με την άλλη μπάσα χορδή (σε διάστημα 5ης ) τα ίδια ακομπανιαμέντα.

Έτσι αν παίζουμε πχ χασάπικο σε τονικότητα D τότε χτυπάμε εναλλακτικά και την μπάσα χορδή Α (ή αν σε Α τότε χτυπάμε εναλλακτικά και την μπάσα χορδή Ε).....
Εξαίρεση αν παίζουμε σε τονικότητα C τότε εναλλακτικά χτυπούμε και την μπάσα Ε πατημένη στο G .Δηλαδή στην περίπτωση του C – G όπου η τονική είναι η C και η άλλη μπάσα θα είναι η G , όμως η μπάσα χορδή είναι η Ε άρα πρέπει το ακόρντο C , αν θέλουμε να παίζουμε μπασοκίθαρο, να το μάθουμε με άλλο ‘’πιάσιμο’’ κι όχι αυτό που δείχνουν τα εικονογραφημένα βιβλία με ακόρντα.
Δείτε το εδώ

http://youtube.com/watch?v=mK7648lb8No

ΣΥΝΕΧΙΖΕΤΑΙ....

[STEFANOS604]

.....ΣΥΝΕΧΕΙΑ ΑΠΟ ΤΟ ΠΡΟΗΓΟΥΜΕΝΟ


Ο ''Κύκλος των 5ων'' και για Μινόρε Αρμονικό
Δείτε πιο πάνω φωτογραφία
Ο ‘’κύκλος των 5ων’’ που δίνεται από όλα τα συγγράμματα και στο Internet είναι όπως αυτός, που μπορείτε να επιλέξετε από τις εκατοντάδες φωτογραφίες του διαδικτύου, στους οποίους απεικονίζονται:

• Στον εξωτερικό κύκλο οι κλίμακες Ματζόρε και
• Στον εσωτερικό κύκλο οι αντίστοιχες Σχετικές κλίμακες Μινόρε Φυσικό

Ο κύκλος ισχύει μόνο για το Συγκερασμένο Σύστημα .Στα άλλα συστήματα (με 5ες μη συγκερασμένες), ο κύκλος γίνεται σπείρα των 5ων (Δείτε παρακάτω ενότητα).Στο ισοσυγκερασμένο σύστημα ο κύκλος κλείνει γιατί οι 5ες είναι χαμηλωμένες, έτσι ώστε ξεκινώντας από έναν φθόγγο και προχωρώντας κατά 5ες, μετά από 12 βήματα επιστρέφουμε στον αρχικό φθόγγο.Το Πυθαγόρειο κούρδισμα πχ δεν κλείνει τον κύκλο κατά 23,46 cents(διάστημα γνωστό ως Πυθαγόρειο κόμμα).Πρωτοδημοσιεύτηκε από τον Γερμανό Johann David Heinichen το 1728. (Γι αυτούς που έχουν προτίμηση το ‘’προς τα αριστερά’’ ας διαλέξουν αυτόν ).
Για να καταλάβουμε τον κύκλο των 5ων εξετάζουμε την ιδέα της καθαρής 5ης και καθαρής 4ης στον Κύκλο.Η καθαρή πέμπτη (Perfect Fifth) μετράει 3 Τόνους και 1 Ημιτόνιο , και κινείται κατά τη φορά των δεικτών ωρολογίου,η δε καθαρή τετάρτη (Perfect Fourth) μετράει 2 τόνους και 1 ημιτόνιο και κινείται αντίστροφα της φοράς των δεικτών ωρολογίου.


Κύκλος των 5ων και Τρανσπόρτο ακόρντων

Κύκλος των 5ων στις Πεντατονικές Κλίμακες

Σημείωση: Αν π.χ., αναφερθούμε στην Α πεντατονική (Α, C, D, E, G) σημαίνει  ότι οι νότες (Α, C, D, E, G) σχηματίζουν την ΜΙΝΟR πεντατονική. Επειδή όμως Πεντατονική  είναι κάθε κλίμακα που σχηματίζεται από πέντε νότες( ΟΠΟΙΕΣΔΗΠΟΤΕ πέντε νότες) αν πχ αντικαταστήσουμε τυχαία την E νότα της Α minor πεντατονικής σε F, τότε δεν  θα έχουμε  minor πεντατονική, θα έχουμε την πεντατονική F G A C D F (F major πεντατονική)
Ακόρντα 2-5-1 jazz & Κύκλος των 5ων
Να αναφέρω, πως οι σχέσεις 2-5-1γράφονται σωστά:για τα ματζόρε  2-5-1: iim7     -  V7     -   Imaj7   ή    Ι(triad) καιγια τα μινόρε     2-5-1: iim7b5 -  V7alt -   Im7      ή    Im(triad)Κύκλος των 5ων και Blues με φυσαρμόνικα



Κύκλος των 5ων και Πνευστά

• Τρομπέτες/Κορνέτες/Τρομπόνια/Σαξόφωνα….

Γιατί οι τονικότητες με σημεία αλλοιώσεως είναι συνήθως με υφέσεις (B-flat instruments ??

• Φυσαρμόνικες:

Γιατί οι φυσαρμόνικες με τονικότητες με σημεία αλλοιώσεως ονομάζονται με υφέσεις εκτός από την F# ;





Κύκλος των 5ων σε ασυγκέραστα συστήματα κουρδίσματος ??

Υπάρχει κάποια σχέση του κύκλου με άλλα συστήματα κουρδίσματος; Κύκλο των 4ων & 5ων έχουμε μόνο σε Συγκερασμένο σύστημα. Στα άλλα συστήματα (με 5ες μη συγκερασμένες), ο κύκλος γίνεται σπείρα των 5ων. Στο ισοσυγκερασμένο σύστημα ο κύκλος κλείνει γιατί οι 5ες είναι ''πειραγμένες'' . Δηλαδή είναι χαμηλωμένες, έτσι ώστε ξεκινώντας από έναν φθόγγο και προχωρώντας κατά 5ες, μετά από 12 βήματα  επιστρέφουμε στον αρχικό φθόγγο. Το Πυθαγόρειο κούρδισμα όμως δεν κλείνει τον κύκλο κατά 23,46 cents (διάστημα γνωστό ως Πυθαγόρειο κόμμα). Αξίζει να δείτε το πινακάκι της παρακάτω φωτογραφίας με τίτλο ‘’Pythagoras Intonation’’ στην ενότητα Πυθαγόρειο κούρδισμα και να αφαιρέσετε 2 οποιεσδήποτε εναρμόνιες και θα βρείτε 23,45 cents (πχ B# - C =23,45-0=23,45 cents ή C# - Db = 113,655 – 90,225= 23,46 κλπ….)



ΣΥΝΕΧΙΖΕΤΑΙ...

[STEFANOS604]

...ΣΥΝΕΧΕΙΑ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΟ


Τροποποίησα τον ‘’Κύκλο των 4ων  & 5ων ‘’
Εισαγωγή:
Οι ΟΠΛΙΣΜΟΙ στις κλίμακες Ματζόρε και Μινόρε


Όλα τα παρακάτω αποτελούν θεωρία κατασκευής των Αρμονικών Μινόρε  και επειδή τα θεωρώ δύσκολα προς απομνημόνευση τα ενσωμάτωσα στον ‘’κύκλο των 5ων’’ όπου θα γίνει φανερό ότι είναι πιο εύχρηστα και ευκολονόητα.


Θα προσπαθήσω με παραδείγματα να εξηγήσω πρώτα το θεωρητικό μέρος και μετά αυτό που σκέφτηκα ότι είναι πολύ πρακτικό (τουλάχιστον στη χρήση που κάνω εγώ): Οι αρχάριοι ας μεταβούν απ ευθείας στο Β’ ΜΕΡΟΣ και αργότερα μελετούν και το Α΄’ ΜΕΡΟΣ.
Α’ ΜΕΡΟΣ
Εμπειρικός τρόπος εύρεσης των Διέσεων μιας κλίμακας.
Αν αρχίσουμε από τη νότα F και απαριθμήσουμε καθαρές 5ες  (F – C – G – D – A – E – B) και αν κατά την απαρίθμηση σταματήσουμε σ’ οποιαδήποτε απ’ αυτές τις 5ες και την ονομάσουμε με δίεση τότε κατά ένα ημιτόνιο ψηλότερα βρίσκεται η ματζόρε κλίμακα που έχει τόσες διέσεις όσες οι 5ες που απαρίθμησα.
1ον παράδειγμα:
Πχ έστω ότι σε μια παρτιτούρα βλέπω 4 διέσεις.
•   Απαριθμώ 4 πέμπτες : F – C – G – D
•   Σταματώ στη D και την ονομάζω D#
•   ένα ημιτόνιο ψηλότερα από τη D# είναι η E
•   Άρα η κλίμακα που έχει 4 διέσεις είναι η Ε ματζόρε
•   Η Ε ματζόρε βλέπω ότι έχει όλες τις νότες φυσικές εκτός από τις 4 αυτές 5ες  δηλαδή έχει με διέσεις τις F# - C# - G# - D#
2ον παράδειγμα:
Πχ έστω ότι σε μια παρτιτούρα βλέπω 3 διέσεις.
•   Απαριθμώ 3 πέμπτες : F – C – G
•   Σταμάτησα στη G και την ονομάζω G#
•   ένα ημιτόνιο ψηλότερα από τη G# είναι η A
•   Άρα η κλίμακα που έχει 3 διέσεις είναι η A ματζόρε
•   Η A ματζόρε βλέπω ότι έχει όλες τις νότες φυσικές εκτός από τις 3 αυτές 5ες  δηλαδή έχει με διέσεις τις F# - C# - G#




Εμπειρικός τρόπος εύρεσης των Υφέσεων μιας κλίμακας.
Αν αρχίσουμε την απαρίθμηση { με την αντίθετη σειρά που απαριθμήσαμε για να βρούμε τις διέσεις μιας κλίμακας δηλαδή  B – E – A – D –G – C – F } δηλαδή αρχίζοντας από τη νότα B και απαριθμήσουμε καθαρές 4ες  και αν κατά την απαρίθμηση σταματήσουμε σ’ οποιαδήποτε απ’ αυτές τις 4ες και πάρουμε την προηγούμενη της (την 5η ) και την ονομάσουμε με ύφεση τότε βρίσκεται η ματζόρε κλίμακα που έχει τόσες υφέσεις όσες οι 4ες που απαρίθμησα.
1ον παράδειγμα:
Πχ έστω ότι σε μια παρτιτούρα βλέπω 3 υφέσεις.
•   Απαριθμώ 3 τετάρτες : B – E – A
•   Σταματώ στην  Α
•   Παίρνω όμως την προηγούμενη της (Πέμπτη) δηλαδή τη Ε και την ονομάζω με ύφεση
•   Άρα η κλίμακα που έχει   3 υφέσεις  είναι η Eb  ματζόρε
2ον παράδειγμα:
Πχ έστω ότι σε μια παρτιτούρα βλέπω 5 υφέσεις.
• Απαριθμώ 5 τετάρτες : B – E – A – D –G
• Σταματώ στην  G
• Παίρνω όμως την προηγούμενη της ( Πέμπτη) δηλαδή την D και την ονομάζω με ύφεση
• Άρα η κλίμακα που έχει  5 υφέσεις  είναι η Db  ματζόρε


Εμπειρικός τρόπος εύρεσης Οπλισμού κλίμακας
1ον παράδειγμα: Πχ η Α ματζόρε τι οπλισμό έχει?
1.    Ο προσαγωγέας της Α είναι το G#
2.   Παίρνω τη σειρά F C G D A E B και σταματώ στην G
3.   Άρα η Α ματζόρε έχει τις αλλοιώσεις F# - C# - G#
4.   H F#m φυσικό  έχει σχετική την Α ματζόρε άρα θα έχει τις ίδιες διέσεις
5.   Επειδή όμως η F#m αρμονικό  είναι Μινόρε Αρμονίας η μεγάλη 3η   της 5ης  είναι η Ε#
6.    Άρα η  H F#m αρμονικό  θα είναι : F#   G#   A   B   C#   D   E#
7.   Αφού η αρμονική F#m είναι Μινόρε  Αρμονίας έχει και προσαγωγέα που οδηγεί στην τονική με βήμα ημιτονίου. Άρα στην περίπτωση της F# είναι η E#




Παράδειγμα 2ον : Πχ η Eb ματζόρε τι οπλισμό έχει?
1.   Παίρνω τη σειρά B E A D G C F και σταματώ στην E και ταυτόχρονα παίρνω και την επομένη που είναι η A
2.   Άρα η Eb ματζόρε έχει τις αλλοιώσεις Bb Εb Ab
3.   Αρα η Eb ματζόρε είναι: Eb F G Ab Bb C D
4.   H Cm φυσικό έχει σχετική ματζόρε την Eb άρα θα έχει τις 3 υφέσεις (Bb Εb Ab) της Eb όμως
5.   Η μεγάλη 3η  της 5ης   είναι η Β επομένως η προηγούμενη Bb πρέπει να γίνει Β
6.   Άρα η κλίμακα της Cm αρμονικό είναι η : C   D   Eb   F   G   Ab   B
7.   Δηλαδή με 2 υφέσεις και όχι με 3 που έχει η σχετική της ματζόρε Εb διότι για να δημιουργηθεί αρμονία πρέπει να υπάρχει το τριτόνιο μεταξύ F – B, ενώ αν διατηρούσε το Bb της σχετικής Eb τότε θα ήταν 2,5 τόνοι και δεν θα υπήρχε αρμονία.
8.   Αφού η αρμονική Cm είναι Μινόρε  Αρμονίας έχει και προσαγωγέα που οδηγεί στην τονική με βήμα ημιτονίου. Άρα στην περίπτωση της C είναι η Β.


Β’ ΜΕΡΟΣ
Όλα τα παραπάνω επειδή τα θεωρώ δύσκολα προς απομνημόνευση τα ενσωμάτωσα στον ‘’κύκλο των 5ων’’ όπου είναι φανερό ότι είναι πιο εύχρηστα και ευκολονόητα.
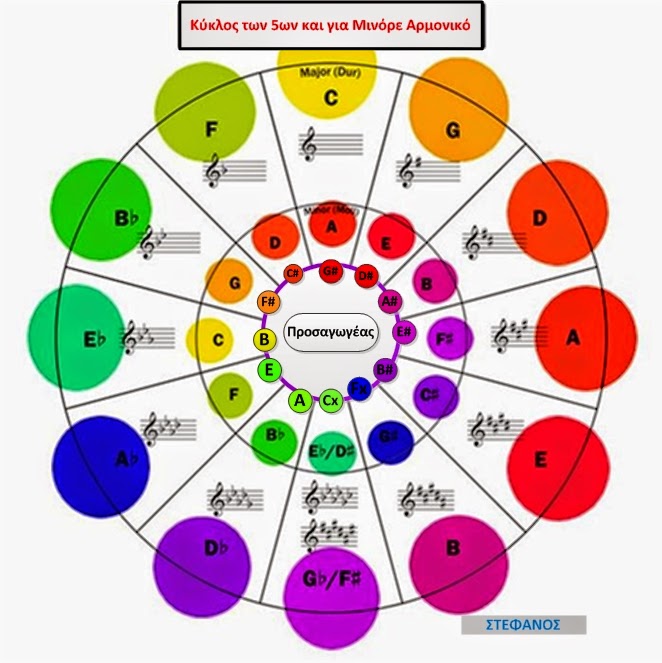
Ο ‘’κύκλος των 5ων’’ που δίνεται από όλα τα συγγράμματα και στο Internet είναι όπως αυτός της φωτογραφίας στην αρχή του άρθρου :
Εγώ απλά τα παραπάνω δύσκολα για να γίνουν κατανοητά απ’ όλους τα ενσωμάτωσα σ’ έναν τρίτο εσωτερικό κύκλο.
Πιστεύω ότι η ενσωμάτωση του εσωτερικού κύκλου δεν δημιουργεί κάποιο πρόβλημα στην όλη δομή του κύκλου των 5ων .

[STEFANOS604]

Έγινε , στο προηγούμενο σχόλιο μου η θεωρητική ανάπτυξη του θέματος και στο μέλλον θα ακολουθήσουν ακόμη κάποιες πληροφορίες

[Guitar Fan]

εξαιρετικό άρθρο,


συγχαρητήρια